From Wikipedia, the free encyclopedia
In mathematics, informally speaking, a sequence is an ordered list of objects (or events). Like a set, it contains members (also called elements, or terms). The number of ordered elements (possibly infinite) is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence. Most precisely, a sequence can be defined as a function whose domain is a countable totally ordered set, such as the natural numbers.
For example, (M, A, R, Y) is a sequence of letters with the letter 'M' first and 'Y' last. This sequence differs from (A, R, M, Y). Also, the sequence (1, 1, 2, 3, 5, 8), which contains the number 1 at two different positions, is a valid sequence. Sequences can be finite, as in this example, or infinite, such as the sequence of all even positive integers(2, 4, 6,...). Finite sequences are sometimes known as strings or words and infinite sequences as streams. The empty sequence ( ) is included in most notions of sequence, but may be excluded depending on the context.
From Wikipedia, the free encyclopedia
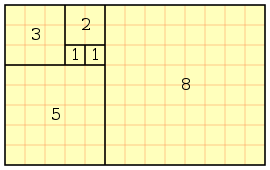
In mathematics, the Fibonacci numbers or Fibonacci series or Fibonacci sequence are the numbers in the following integer sequence:[1][2]
By definition, the first two numbers in the Fibonacci sequence are 0 and 1, and each subsequent number is the sum of the previous two.
From Wikipedia, the free encyclopedia
In mathematics, the limit of a sequence is the value that the terms of a sequence "tend to".[1] If such a limit exists, the sequence is called convergent. A sequence which does not converge is said to be divergent.[2] The limit of a sequence is said to be the fundamental notion on which the whole of analysis ultimately rests.[1]
Limits can be defined in any metric or topological space, but are usually first encountered in the real numbers.
No comments:
Post a Comment