Sequences & Series - Wikipedia et al Links

Sequence
From Wikipedia, the free encyclopedia

Google

In mathematics, informally speaking, a sequence is an ordered list of objects (or events). Like a set, it contains members (also called elements, or terms). The number of ordered elements (possibly infinite) is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence. Most precisely, a sequence can be defined as a function whose domain is a countable totally ordered set, such as the natural numbers.

For example, (M, A, R, Y) is a sequence of letters with the letter 'M' first and 'Y' last. This sequence differs from (A, R, M, Y). Also, the sequence (1, 1, 2, 3, 5, 8), which contains the number 1 at two different positions, is a valid sequence. Sequences can be finite, as in this example, or infinite, such as the sequence of all even positive integers(2, 4, 6,...). Finite sequences are sometimes known as strings or words and infinite sequences as streams. The empty sequence ( ) is included in most notions of sequence, but may be excluded depending on the context.

Fibonacci Sequence

From Wikipedia, the free encyclopedia

A tiling with squares whose side lengths are successive Fibonacci numbers

An approximation of the golden spiral created by drawing circular arcs connecting the opposite corners of squares in the Fibonacci tiling; this one uses squares of sizes 1, 1, 2, 3, 5, 8, 13, 21, and 34.

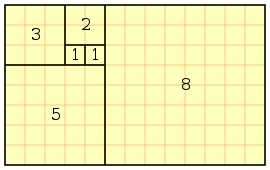
In mathematics, the Fibonacci numbers or Fibonacci series or Fibonacci sequence are the numbers in the following integer sequence:^[1][2]

 (sequence A000045 in OEIS)

By definition, the first two numbers in the Fibonacci sequence are 0 and 1, and each subsequent number is the sum of the previous two.

Convergent/Divergent Sequence (Limit of a Sequence)

From Wikipedia, the free encyclopedia

In mathematics, the limit of a sequence is the value that the terms of a sequence "tend to".^[1] If such a limit exists, the sequence is called convergent. A sequence which does not converge is said to be divergent.^[2] The limit of a sequence is said to be the fundamental notion on which the whole of analysis ultimately rests.^[1]

Limits can be defined in any metric or topological space, but are usually first encountered in the real numbers.

Fundamental Theorem of Calculus

If, in fact, "The Fundamental Theorem of Calculus" is fundamental, why is it on page 400.  It should be on page 1.  - Can you see the forest for the trees?

Starting calculus with the Fundamental Theorem (FTC) is impossible!  Right?  You must go through the normal progression of functions, limits, derivatives, etc., before introducing such complexity.  Right?  Perhaps not.  The standard approach takes weeks or months before integration is discussed.  In the meantime you're wondering how difficult integrals will be as you struggle with derivatives.  With FTC, on day one, you're dealing with the "forest," the big picture.  It will (should) demystify the entire subject.

Look what you can achieve by examining the above image.  Work backwards.  This is what a function looks like; here's a derivative/slope/tangent; this is a limit and this is how it's used; this is an area function, this is why the derivative of the area function/integral = y = f(x).

Explain the symbology; explain the terminology.  Remember, "The Fundamental Theorem of Calculus" is fundamental!  There's no rush.  Take your time.  Explain each concept while tying them into a cohesive whole.

FTC links